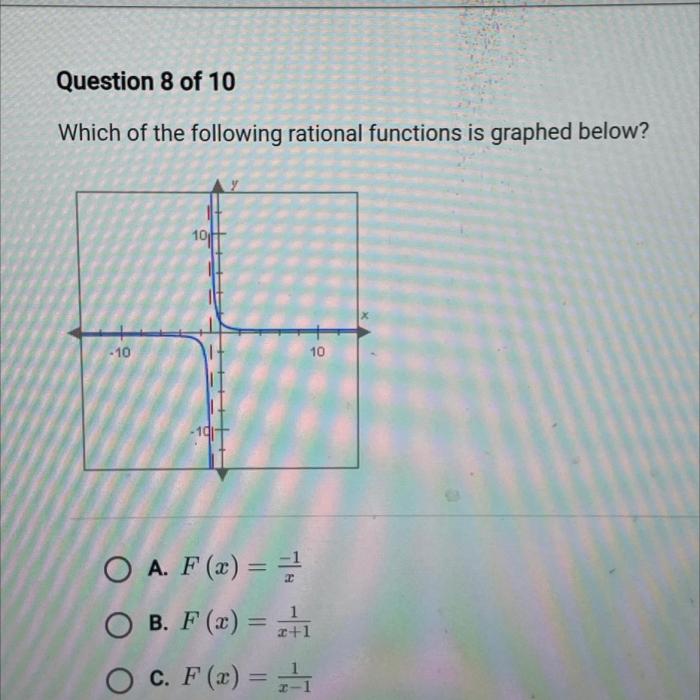
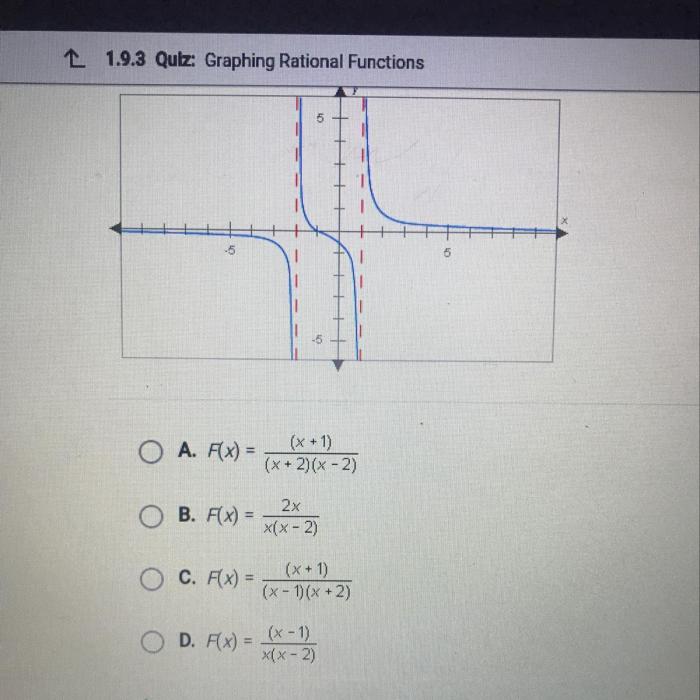
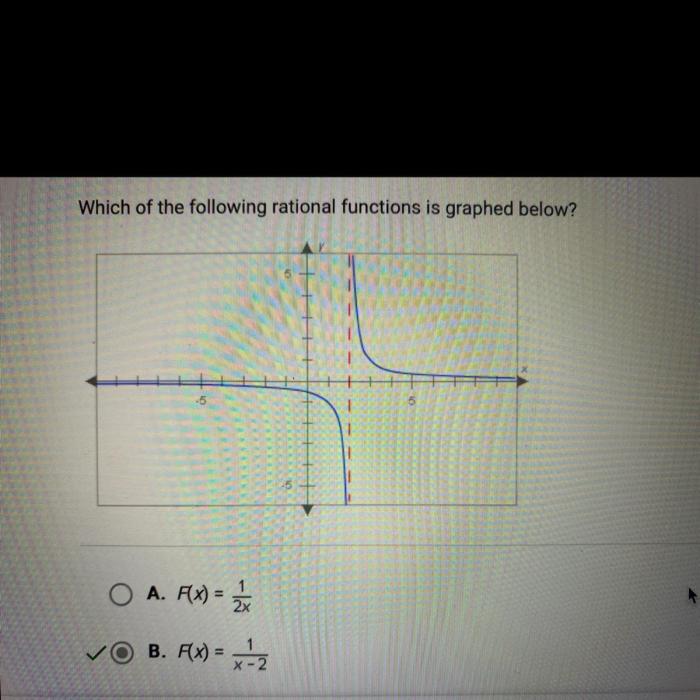
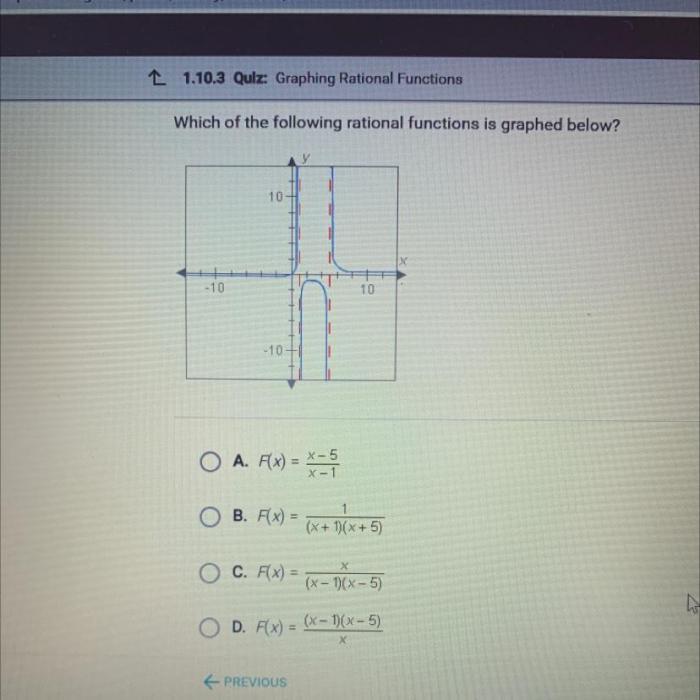
Which of the following rational functions is graphed below 10? This question takes center stage in this exploration of rational functions, where we will delve into their concept, types, and behavior, ultimately identifying the specific function represented by the given graph.
As we embark on this journey, we will dissect the graph’s key features, establish its relationship with the rational function, and pinpoint any notable points of interest. Through a comprehensive analysis of the function’s behavior, domain, range, continuity, and differentiability, we will gain a thorough understanding of its characteristics.
Rational Functions and Their Graphs
Rational functions are mathematical expressions that represent the ratio of two polynomials. They are used to model a wide range of phenomena, including the behavior of physical systems, the growth of populations, and the flow of fluids.
Rational functions can be classified into several types, depending on the degrees of the polynomials in the numerator and denominator. The most common type of rational function is the linear-quadratic rational function, which has a linear numerator and a quadratic denominator.
The graph of a rational function can be determined by plotting the points (x, f(x)) for various values of x. The graph will typically have a number of key features, including:
- Intercepts: The points where the graph crosses the x- and y-axes.
- Asymptotes: The lines that the graph approaches as x approaches infinity or negative infinity.
- Holes: The points where the graph is undefined.
The behavior of a rational function can be analyzed by examining its graph. The graph will typically show how the function increases or decreases as x increases or decreases, and it will also indicate the function’s domain and range.
Rational functions are a powerful tool for modeling a wide range of phenomena. By understanding the key features of their graphs, we can gain insights into the behavior of the systems they represent.
FAQ Compilation: Which Of The Following Rational Functions Is Graphed Below 10
What are rational functions?
Rational functions are functions that can be expressed as the quotient of two polynomials, f(x) = p(x) / q(x), where p(x) and q(x) are polynomials and q(x) is not the zero polynomial.
How do I identify the rational function represented by a graph?
To identify the rational function represented by a graph, you can examine its key features, such as intercepts, asymptotes, and the behavior of the graph as x approaches infinity and negative infinity.
What is the domain and range of a rational function?
The domain of a rational function is the set of all real numbers except for the values that make the denominator zero. The range of a rational function is the set of all real numbers.